暮らしを豊かにする、代数方程式の考え方

投資の初心者
投資の用語で出てくる「代数方程式」って、難しそうな名前ですが、具体的にどんなものなんですか?連立方程式ともいうとありますが、投資とどう関係するのかイメージがわきません。

投資アドバイザー
なるほど、代数方程式という言葉に戸惑っていますね。ご安心ください。代数方程式は、簡単に言うと、未知の数(XやYなど)を含む数式のことです。そして、連立方程式は、複数の代数方程式を組み合わせて、それらの未知数を同時に求めるものです。投資の世界では、将来の利益やリスクなどを予測するために、この代数方程式や連立方程式が使われることがあります。

投資の初心者
将来の利益やリスクを予測するために使うんですね。例えば、どんな場合に使うんですか?具体的な例を教えていただけますか?

投資アドバイザー
良い質問ですね。例えば、ある企業の将来の売上高を予測したいとします。過去の売上データや市場の成長率などを使って、売上高をXという未知数で表した代数方程式を作ります。さらに、企業のコストや利益率など、他の要素も考慮して複数の代数方程式を作り、連立方程式として解くことで、より正確な将来の売上高を予測できる、というように使われます。もちろん、これはあくまで一例で、実際にはもっと複雑なモデルが使われることもあります。
代数方程式とは。
「投資」の分野で使用される『代数方程式』とは、未知数を用いて計算を行う数式のことです。複数の未知数を含む場合は、連立方程式と呼ばれることもあります。
代数方程式とは何か

代数方程式とは、未知の数(通常は文字で示されます)を含む等式のことです。これは、小学校で学んだ算術を発展させ、未知の値を特定するための道具となります。例えば、「ある数に3を足すと5になる」という状況を「X + 3 = 5」という式で表すことができます。この式を解くことで、Xが2であるという答えを見つけ出せます。
代数方程式は、一つだけでなく、複数の未知数を含む連立方程式としても存在します。連立方程式は、複数の条件が組み合わさった問題を解く際に役立ちます。例えば、ある品物の価格と数量の関係を表す二つの方程式を連立させることで、それぞれの価格と数量を同時に求めることが可能です。
このように、代数方程式は、私たちの身の回りの様々な問題を解決するための基礎となる考え方です。複雑な現象を数式で表現し、その数式を解くことで、隠された真実を明らかにすることができます。代数方程式は、数学の世界だけでなく、物理学、経済学、工学など、様々な分野で応用されています。未知の現象を解き明かすための強力な手段として、現代社会において必要不可欠な存在と言えるでしょう。
| 項目 | 説明 |
|---|---|
| 代数方程式とは | 未知数を含む等式。未知の値を特定する道具。 |
| 例 | X + 3 = 5 |
| 連立方程式 | 複数の未知数を含む方程式。複数の条件が組み合わさった問題を解く際に役立つ。 |
| 応用 | 物理学、経済学、工学など |
| 重要性 | 未知の現象を解き明かすための強力な手段として、現代社会において必要不可欠。 |
連立方程式の活用例

連立方程式は、私たちの生活や仕事の中で、色々な要素が複雑に関係している問題を解くのに役立つ道具です。例えば、会社が二つの商品を作るとき、それぞれの商品の材料や作る時間が違うとします。使える材料や時間には限りがあるので、連立方程式を使って、一番利益が出るようにそれぞれの商品の数を決めることができます。また、日常では、違う利率の預金口座にお金を預けている人が、全体の利息を一番多くしたい場合に、どの口座にいくら預けるかを決めるのに使えます。旅行の計画でも、飛行機や電車の費用と時間を考えて、予算内で一番良いルートを見つけるのに役立ちます。このように、連立方程式は、色々な制限がある中で、一番良い答えを見つけるための強い味方です。複雑な問題を整理して、数式で表すことで、より客観的に判断し、良い決断ができるように助けてくれます。
| 場面 | 連立方程式の活用 |
|---|---|
| 会社の製品計画 | 材料や時間の制約下で、利益が最大になる各製品の生産数を決定 |
| 預金口座の配分 | 異なる利率の口座間で、全体の利息を最大化するための預金額を決定 |
| 旅行計画 | 予算内で、費用と時間を考慮して最適なルートを決定 |
お金の計画における応用

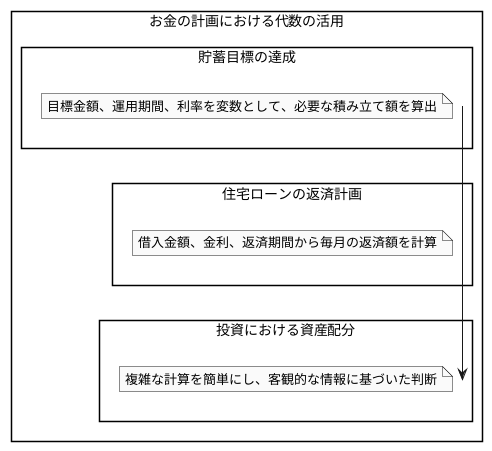
お金の計画を立てる上で、代数の考え方は非常に有効です。たとえば、将来達成したい貯蓄目標を設定し、それを実現するために毎月いくら積み立てる必要があるかを計算する際に役立ちます。目標金額、運用期間、利率などを変数として使い、方程式を解くことで、必要な積み立て額を算出できます。また、住宅ローンの返済計画を立てる際にも、借入金額、金利、返済期間などを考慮して、毎月の返済額を計算することができます。さらに、投資においては、異なる危険性と収益性を持つ資産を組み合わせ、目標とする収益を達成するために、最適な資産の割り振りを決定する際に、代数の知識が活用できます。このように、代数は、将来の目標を達成するために、今どのような行動を取るべきかを具体的に示す道具となります。不確実な将来に対し、計画的に準備を進めるために、代数の考え方を積極的に取り入れることが大切です。複雑な計算を簡単にし、客観的な情報に基づいて判断することで、より効果的なお金の計画を立てられます。
複利計算と方程式

資産を殖やす上で欠かせない考え方である複利は、代数方程式で分かりやすく説明できます。複利とは、最初に預けたお金(元本)から得た利息を元本に加えて、次の期間では増えた元本に対して利息が付く仕組みです。この効果により、長期間の資産運用では、元本だけでなく利息も増え、大きな成果につながります。
複利計算の基本式は、将来の資産価値 = 元本 × (1 + 利率)^運用期間です。例えば、100万円を年利5%で10年間運用した場合、複利で計算すると約163万円になります。これは、単利で運用するよりも大きな差です。時間が長ければ長いほど、複利の効果は大きくなります。
代数方程式を使うことで、複利の効果を具体的に理解し、将来に向けた資産形成の計画を立てるのに役立ちます。複利の力を最大限に活かすためには、早めに資産運用を始め、長い目で投資することが大切です。
| 項目 | 説明 |
|---|---|
| 複利 | 元本に利息を加え、その合計にさらに利息が付く仕組み |
| 複利計算の基本式 | 将来の資産価値 = 元本 × (1 + 利率)^運用期間 |
| 複利のメリット | 長期間の資産運用で大きな成果につながる |
| 複利を活かすために | 早めに資産運用を始め、長期的な視点を持つ |
生活設計への応用

数式的な思考は、日々の金銭管理は勿論のこと、より広い視野で人生を考える際にも役立ちます。例えば、結婚や出産、住宅の取得、お子様の教育といった人生における大きな出来事のために、将来必要となる資金を予測します。そして、それを達成するために、いつ、どのような方法で貯蓄や投資を行うべきかを具体的に計画できます。また、退職後の生活に必要な費用を算出し、公的な年金に加えて、どれくらいの資産を準備する必要があるかを把握することも可能です。さらに、仕事における目標を定める際にも、数式的な考え方は有効です。異なる職務を選んだ場合に収入がどのように変化するかを予測し、将来の目標を達成するために、どのような能力を身につけ、どのような経験を積むべきかを検討できます。このように、数式は将来の目標を達成するために、今、何をすべきかを具体的に示す道具となります。人生は常に変化するため、定期的に計画を見直し、必要に応じて修正することが大切です。数式を用いることで、変化に対応しながら、柔軟に人生設計を進めることができます。
| ライフイベント | 数式的な思考の活用 |
|---|---|
| 結婚・出産 | 将来必要な資金の予測、貯蓄・投資計画 |
| 住宅取得 | 将来必要な資金の予測、貯蓄・投資計画 |
| 子供の教育 | 将来必要な資金の予測、貯蓄・投資計画 |
| 退職後の生活 | 必要な費用の算出、年金以外の資産準備 |
| 仕事の目標設定 | 収入の変化予測、必要な能力・経験の検討 |
